在OpticStudio中，TrueFreeForm面屬於序列模式下的一種面型。此表面結合了多項式(Polynomial)和網格矢高兩種面型的特性。以TrueFreeForm面進行設計時，我們還可以把網格矢高中的每個點作為目標，並且以非參數化(non-parameterized)的方式進行矢高的優化。當使用者想以局部區域為優化目標，或是多項式函數無法完整呈現矢高架構時，TrueFreeForm面會是一個好的選擇。

在使用TrueFreeForm面進行設計時，我們能以多項式函數的型式，如雙錐 toroidal (biconic toroidal)、偶次項非球面(even asphere)、Zernike標準矢高(Zernike standard polynomial)、擴展多項式(extended polynomial)以及網格矢高定義的方式設定矢高。在同一個表面以多種函式定義可以為我們的設計過程來一些好處，例如原先以擴展多項式(extended polynomial)、雙錐 toroidal (biconic toroidal)或網格定義(grid-based definitions)為目標進行的自由曲面優化，現在可用Zernike係數對不規則的設計進行額外的公差分析。此外，我們還可以將網格矢高上的各點設為變數進行矢高的優化，這是以TrueFreeForm面進行設計時較有趣的一點。

相較於參數式(parametric)優化，網格矢高優化具有許多優點。由於預設的網格矢高內插演算法是以雙三次樣條(bicubic spline)的方式進行計算，因此值域中的每個點隻會對網格中相鄰的至多兩點產生影響。假如我們針對資料中的一點進行優化，則系統只會改變局部的表面結構，距離較遠的表面資料則會維持原樣。下圖顯示了一個簡化的一維平滑曲線模型。圖中的三條曲線分別以5個點定義出三次樣條(cubic spline)。我們可以看到圖中最左邊的點會在三條曲線間移動，但只會對距離最近的兩點產生影響。

接著，我們利用下圖將上述概念推廣到二維空間。我們先以二維網格的矢高值表示目標的表面結構，並選擇其中一點進行矢高的優化(圖中紅點)，可以看到只有藍色方形(5x5個點)內的區域會受到影響。

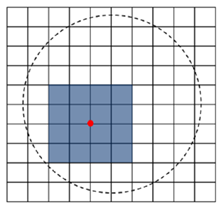
以上的例子告訴我們兩件事：

第一，以網格矢高的方式進行優化，我們可以將優化目標限制在局部的區域中；相對的，使用參數式優化時，每當我們對單一數值進行變更，則整個表面的結構均會發生變化。
第二，我們可以較輕易的產生特殊的表面幾何關係，而這是我們使用有限次的多項式函數難以達到的。

在使用網格矢高優化時有兩點需要特別注意。由於矢高網格會運用到三次方的內插法(cubic interpolation)，這代表由一組資料點所產生的曲線會受到幾何關係的限制。此外，用於定義網格的矢高資料量也是進行優化時重要的考量。資料點太多會降低優化的效率(變數過多)，且會對取樣產生負面的影響(在接下來的篇幅中詳述)。另一方面，若系統以過少的資料點進行優化，將難以產生最佳的優化表面。因此，在使用網格矢高的方式進行優化前，我們需要更謹慎的設定網格的參數。

OpticStudio的TrueFreeForm 模型為相關的設計提供了更高的自由度，包括了多重自由曲面矢高的定義，和以網格的方式進行表面矢高的優化。

了解更多此功能, Zemax 客戶可登入 MyZemax.com 平台閱讀完整文章，或是聯繫我們的業務代表以了解更多 OpticStudio。

相關內容
一种全新的自由曲面优化方法 ——TrueFreeForm™ 优化 webinar (on-demand)
OpticStudio 20.3 一次速度的全面革新 webinar (on-demand)